漫谈力学
漫谈力学
认识力学,不应该把力学孤立出来单独理解。力学的本质与特征是通过与相关学 科的比较逐渐形成并明晰的。力学与数学、工程有着天然、不可分割的紧密联 系,与数学学科相比,力学是应用学科;与工程学科相比,力学是几乎所有工程 学科的理论基础,具有自然哲学的研究传统;正是这种特性使力学成为了数学与 工程得以互通的桥梁。
其次,对力学的理解不应是一成不变的。准确的说,力学也是一个历史的概念, 它的内涵随时代的变化而不断发生变化。亚里士多德时代,力学与数学无关,是 纯粹的思辨;伽利略将数学定量分析应用于运动学开始,力学才变成了精密科 学;直至牛顿力学、拉格朗日分析力学的建立,力学的发展程度越高,与数学的 联系也越加紧密。
随着时代的发展,越是大型工程对力学分析的依赖越高,大型舰艇、大跨度桥 梁、超高建筑、高铁、空间技术等等领域越来越依赖于力学理论的发展。本文首 先将力学视为数学、工程之间的桥梁,讨论力学与数学、工程之间的紧密联系, 然后简述力学各分支学科的发展,以此构建力学的基本框架。
一、力学与数学的密切联系
数学和力学这两个学科,有点像亲姐妹一样,她们结伴成长。在历史发展的长河 中,主流数学和力学的发展总是同步的。最著名的数学家一般也是最著名的力学 家。
——武际可《最著名的数学家一般也是最著名的力学家》

阿基米德 (Arch imedes, 前 287 年 前 212 年) ,确 立了流体静力学的基本原理
(阿基米德定律) ,提出了杠 杆原理等,被后人誉为 ”力 学之父”。
在数学上 ,他给出曲线 围成简单图形的体积和重心 的计算方法,从而引进了简 单的极限概念。

牛顿 ( Isaac Newton ,
1643 1727) ,力学上发现 了万有引刀;提出的牛顿三 是律成为经典力学的墓础;
《自然哲学的数学原理》 成 为力学发展史的里程碑。
数学上发现了二项式 走理,创立了微积分,在解 析几何、数僵方法等数学领 域中均有丰硕的成就。
![]()

二、力学与工程的密切关系
从过去100年来力学发展情况看,力学是一门处理宏观问题的学问。它是用理 论,通过具体数字计算一个个实际问题。这些问题在过去都来自工程。
——钱学森《我对今日力学的认识》

团军团

-
纳维 (Claude-LouisNavier , 1785年 1836 年) ,法国刀学家,
1824-1826 年,采用理论计算设计
了一座悬索桥,改变了桥梁工程领 域单凭经验设计建造用桥的传统。 上图为纳维设计的悬索桥,及翼桥 墩部台。

三、牛顿力学的创立
从古希腊自然哲学到17世纪力学发展,主要以天体力学和牛顿力学为代表, 1687年牛顿发表《自然哲学的数学原理》,标志着牛顿力学的确立。

亚里士多德 (A 「istotl e,前 384前 322) :是古希腊自然 哲学发展的集大成者,{刨寄自然哲学进行了台科,使得科学 的发展有了学科针对性。在力学方面的贡献主要集中在 《物 理学》 中,尽管存在一些错误的结论,但翼学术思想对于力 学学科的发展具有重要的价值和意义。
![]()


伽利路 (Galile。Galilei ,1564 ”1642) 是淫生盖亚里士多德物理学与宇领刀学的班要人物,比
萨斜塔吉9);;体与斜面实主盘震动了汪里立多德的权威,总结出自由落体定律、惯锥律和伽利路馆 对性原理等推翻了亚里士多德物理学的许多撼断.奠定了经典刀学的基础,而他将定量分析引
入实验,便提成为近代实验科学的奠基人 被誉为 ”近代为学之父”,为年预理论体系奠定了基础.
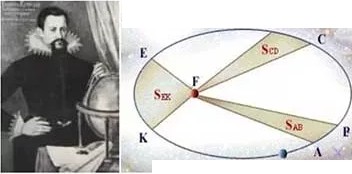
Jt骨弱和付芷梳阿拉总。 开窗勒(J。hannes Kepi町,
1571-1630) 行星运行三定
律.
1.每一个行墨都iB备 白的键因轨道环绕太阳.而 太阳缸子衡阳?个焦.r#a;
2. 在德等时间内,太
阳租运动中的行星的连线
3. 绕以太阳为焦点的确囚轨iti运行的行罢,只椭圆轨il:i半t是
$曲的立方与周期的平方之比是一个常st.
{向量半径} 所组泣的面积 徊等;
![]()

四、最速降线与变分法
约翰∙伯努利 (Johann Bernoulli, 1667~1748) 1696年向全欧洲数学家挑战,提 出一个难题:“设在垂直平面内有任意两点,一个质点受地心引力的作用,自较 高点下滑至较低点,不计摩擦,问沿着什么曲线下滑,时间最短?”科学家对该 问题的研究导致了变分法的诞生!


1630 年,伽利略在做斜面实验时发现,两个相同的4
£从起 f青·
向终点,最快的路径并不是直线而是一条曲线。
E伽利略错误的认为是圄的一部分。
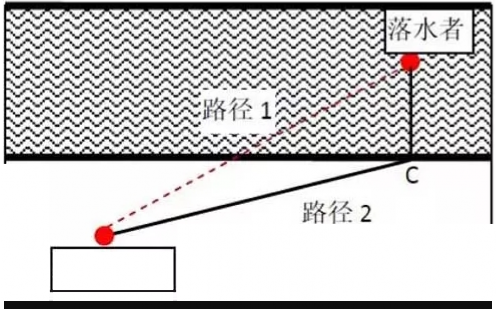
施救人员
为了说明这个问题,先来看一个河中救人的 例子。假设左国申奇人落水,为了尽快将人求出, 施救人员一般会先在岸上跑到距离落水者最近 的 C 点,然后在跳入水中游泳到达落水者处, 即选择路径 2 进行施放。而不是选择直线路径 1 进行施救。这是因为陆地上跑的快,就多跑一段, 游泳的速度慢就少游一段。因此,路径与速度密 切直接相关。
![]()

五、刚体运动的描述
牛顿力学主要解决了质点运动和相关力学问题,而刚体力学主要是在1765年欧 拉发表的《刚体运动理论》后逐渐形成并发展起来的。
![]()
![]()
‘
..

r 、
![]()
, //
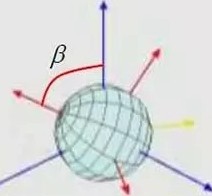
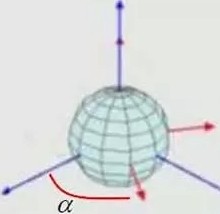
欧拉 (Leonhard Euler, 1707-1783 ) 最阜 ( 1760 年) 用进动角、章动角和自转角 (合称欧拉角) 描述了刚体在 三维欧氏族空间的绕定点运动。如上国所示,α 为进动角, F为童动角,y 为自转角,并给出了刚体绕定点的运动方程。
A, B气 C 分别为刚体 对伴 随坐标 系 二个 坐标 轴的转动惯量 ,(I);I.; 角速 度向堂,其在伴随坐标系 中的分量分别为 p , q,,.
4巾B )q r叫
B铲(μ)ψ]11 2
C +(B - A) pq =1'vf 3
dt
![]()

六、分析力学的发展
分析力学是有别于牛顿力学体系的新体系,其特点是对能量与功的分析代替对力 与力矩的分析。1788 年,拉格朗日完成的《分析力学》标志着分析力学体系的 建立。



1725 年约翰 伯努利:在一切 力的平衡中,不论它们如何 作用.正能量的第I将总是等 于负能量的总和。
19 世纪初J科里奥利给出的 功原理描述:在迎想完整的 约束中,主动力在位移上 所作的总功为零。
1743年达朗贝尔提出了求解 约束系统动力学问题的一个 普遍原理一达朗贝尔原理。
在分析力学中,虚功原理、达 朗贝尔原理成为两大革妥理 论基础。

七、连续介质力学-流体力学
流体力学的发展大致可分为四个阶段:
![]()
萌芽阶段(16世纪以前);
![]()
形成阶段(文艺复兴-18世纪中叶);
![]()
发展阶段(18世纪中叶-19世纪中叶);
![]()
流体力学的飞跃发展(19世纪中叶以来)。
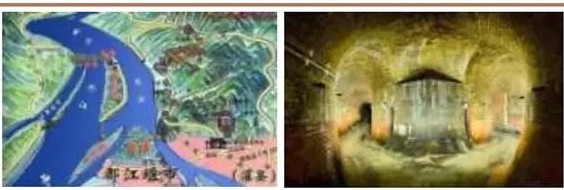
2100 年后,f/7 可饮用的都江』桂元2500 年后仍可伙刑的罗马砍下 分利 用了 弯i革坏 瓦排沙 水 革 系统
在萌芽阶段,流体利用主要以水利、造船等工程为依托, 人们逐渐和累流体力学的知识经验,如中国的都江垣,罗马 古城的下水道系统,在今夫看来都非常先进 .

![]()
公元前 250年,阿基米德的 《论浮力》 丑于流体力学进 行了较为系统的总结,奠定了流体力学的基础。

八、连续介质力学-固体力学
固体力学的发展是从弹性力学开始的,推动固体力学的发展主要有两个方面:
![]()
一方面是工程的推动,桥梁道路建设、造船、军械制造等迫切需要了
解固体的变形与破坏的机理;
![]()
另一方面,是对光波传播机理的探讨要求了解弹性波的传播理论。


![]()
![]()
响 。
,窜耐’
-翅舶喃自曲 曲嗣,o r...向隅,。,
审qilllldk 帽r1n& IO四”
,回 归田阳时 帽Foiff回电阳也..1, l,y
胁 m,均F曲唱 帽均 e;r •!irk‘四 问叫
I rER-L:l fJ
。
旺乓沙”
N
ft剧协· :le
叩可丘,'!,
d回国如....蛐1肘 ...., be,dl....lJho.t la恻翩翩s
r ,.n
m<loo "'-飞 回帽(cq阻四 曲’“陋 刚刚阳,
-,,,dIla.I田G,. I 翩翩咽,副总t量:11 WIU
M晶S -
伽利略 《关于两门新科学 1678 年,胡克在 的对话》 ( 1638年) 申研究悬 《论弹簧》 中指出, 譬梁的强度,暗示中性层位于在弯曲时杆的一侧
梁的下面。 的纤维伸长,另寸则
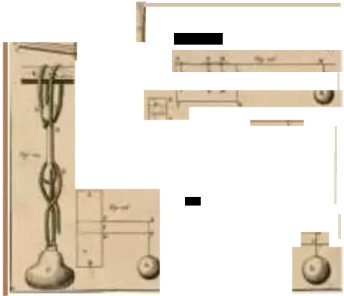
』 专r 品 副 被压缩。
1686 年,马路
. .丰 -"
·γiii " 上|
气r ;走|
特在 《论水和;民他
流体的运动》 中也
门战 | 认为中性层在梁的
c t-= I 下侧,但具体位置
与伽 利 略高所 不
同。
马略特的插图
![]()

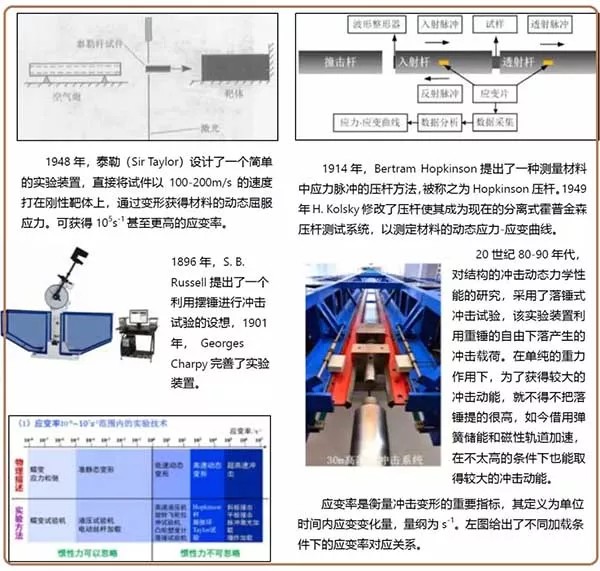
九、冲击动力学
冲击碰撞是日常生活中常见的力学现象,同时又与航空航天、汽车、防护工程、 国防工程息息相关。冲击动力学是专门研究在短暂而强烈的动载作用下材料行为 和结构响应的一门科学。
![]()
![]()
h

A · ↓ .B
最初人们采用冲击动载荷系数,将冲击
问题等效为静力学|可题来处理:
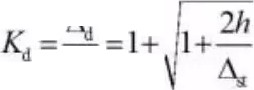

/ ![]() 巳在饭
巳在饭
![]() 捻E马
捻E马
![]()
饵’t rt码血
1872 年,John Hopkinson 为了测走钢丝在 冲击加载下的强度,在剑桥大学工程实验室设计 了一个演示实验。如上国左,讨论硅码下落高度 对钢丝断裂特性的影响,发现当下落高度不太高 时,上端断裂 ,太高时下端断裂。
![]()
十、非线性科学的发展
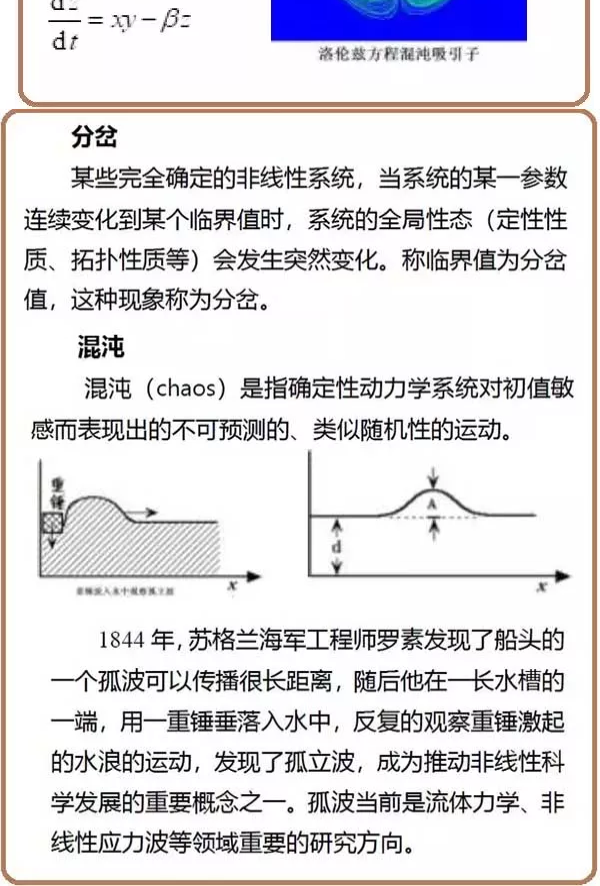
迄今为止,我们处理的问题多以线性为主,线性系统的整体性态通常满足叠加原 理,从而比较容易分析,但也限制了它的适用范围。在自然科学和工程技术里, 不少现象不能采用线性模型描述。非线性就是不满足线性叠加原理的性质。人们 真正关注的,是仅用线性理论所不能解释的那些非线性现象。非线性科学就是研 究各类系统中非线性现象共同规律的一门交叉科学。

非线性科 学中较成 熟的部分是非线性动力 学。1881 年,法国数学家、
力学家亨利 ·庞加莱 (Jules HenriPoincare ,1854
-1912) 发表的关 于微分
方程所确定的积分 曲线 的论文开创了非 线性 问 题的定性理论研究 。
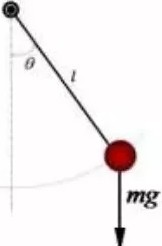
。 单摆是一种理 想、的
物理模型,当摆角小于 5。 时,其运动微分方程可近 似为线性方程 。当单摆做 大幅度摆角运动时,其运 动微分 方程为如下的 非 线性方程:
diθ d θ 、 酣
一.....,,.... +2 β一一 +u..J"" sin θ=0
dt' ’ dt ”
![]()
![]()
1918 年,Georg Duffi暗(1861-1944) 在经典 力学中引入了一个描述具有驱动力单摆的非线 性 动力学方程,成为非线性系统的经典方程杜芬
方程:
d1 xd x.’‘‘ 【
ι÷
+Y 二二K ·.℃+c,扩=F cos Ot d t .d t
此方程可以产生典型 的倍二周期分岔现象。
口·tLJ.:f 方缸倍阴阳分岔 口’
OT
Q r,
![]()

:i:: _Y-;;,t:
t
"“."::)
•..
-a Ia
0:1
!!1


句.,
缸’
![]()
nL
咂岛lh1 O tu,。”I It1 1 ’ ., q.,.
a俨
寸lJ
、
I
-
y
/币、
σ
一-
x-t
d-d
1963 年,美国气象学家浩伦兹(巳 N. Lorenz) 将描述大气热对流的非线性偏微分方程组通过傅 里叶晨开,大胆地截断而导出了描述垂直速度、 上下温差的晨开系数 x( t) ,y( t),z(t)的三维自治动力 系统。该系统对初僵非常敏感,j备伦兹当年只是 忽略了小数点4 位以后的数值,得到的结果就有 了相当大的偏差,甚至是完全相皮。这一初值敏 感性被形象地称为’蝴蝶效应\ 巴西蝴蝶扇动翅 膀在美国引起德克萨斯的隐凤。

、.
、、,/
Z
-
p
/IK
元
=
-
-
t
v
v
a
d
d
...I -
十一、力学的交叉学科
20世纪以来,力学的发展与其它学科的交叉和融合日显突出,形成了许多力学
交叉学科,如生物力学,环境力学,交通力学,爆炸力学等,同时,人类社会和 经济发展的更高需求将不断促进力学与其他学科的交叉,促进力学交叉学科发展 到一个崭新的阶段。
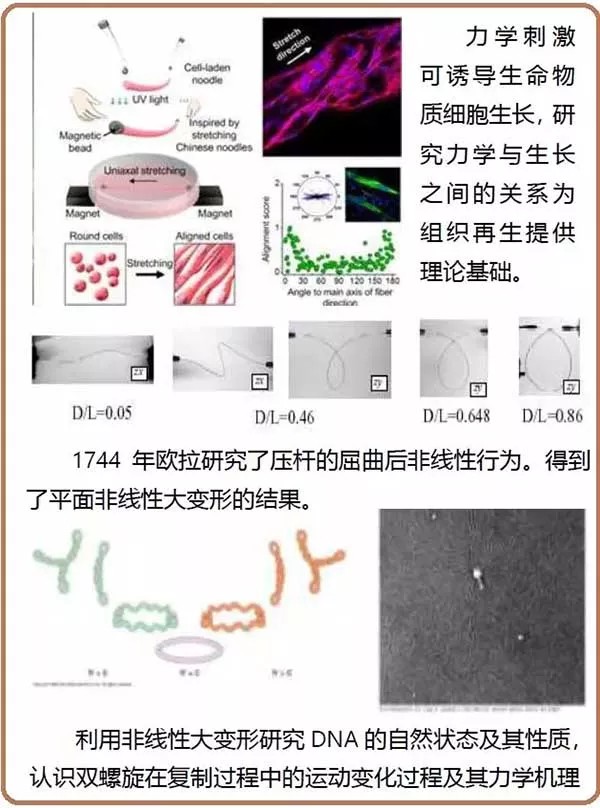

结束语
基尔霍夫说:“力学是关于运动的科学。”如果把静止也看作是运动的一种特殊 形式,世界上的万物已经找不出除了静止和运动还会有什么状态,力学为认识这 些物质(或物体)的状态提供了基本完备的方法,力学广泛的适应性使得力学具 有了自然哲学的属性。
力学到底在人类科技进展中扮演着什么样的角色?
在那些里程碑式的科技进步中,如蒸汽机代表的蒸汽时代,电力代表的电气时 代,信息代表的信息时代,以及人们预测的以互联网、智能技术、生物技术为代 表的新一轮技术革命所催生的新一轮产业革命,似乎力学都没有参与。
其实不然,蒸汽机技术的成熟得益于牛顿力学的完善;电气时代得益于发电机和
电动机的发明,而熟悉发电机和电动机工作原理的人可能不会说与力学无关,电 子工程师们也调侃“如果没有掉入力学和热学的坑里都不好意思说自己是电子工 程师”,信息技术可以分为硬件和软件两个部分,硬件自然少不了力和热,软件 编程部分也会利用力学模型去规划算法;人工智能是新一轮产业革命中重点领 域,而提到人工智能很多人会和信息技术、软件编程相联系,以机器人技术为 例,如果没有力学先规划出机器人的功能动作,并给出这些动作的数学描述,信 息技术和编程就无法开展。
这大概就是马克思所谓的“力学是‘大工业的真正科学的基础’”(《剩余价值 理论》第二册,116)。很多工程问题随着讨论的深入,一般都会成为力学问 题,力学问题解决了,其它问题也就迎刃而解。可能正因如此爱因斯坦说:“尽 管我们今天确实知道古典力学不能用来作为统治全部物理学的基础,可是它在物 理学中仍然占领着我们全部思想的中心。”(《物理学与实在》)
